FISIKA - Penjumlahan Vektor

Menggambar Penjumlahan atau selisih dua buah vektor dengan metode segitiga

Pada kesempatan ini Fisika Asyik akan membahas tentang cara penjumlahan besaran fisika Vektor.

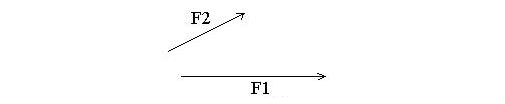
Misalkan dua orang anak mendorong sebuah benda dengan vektor gaya masing-masing sebesar F1 dan F2, seperti ditunjukkan diagram di bawah. Ke arah mana benda itu akan pindah ? 

tentu saja benda tersebut tidak berpindah searah F1 atau F2. dalam kasus seperti itu, maka benda tersebut berpindah searah dengan F1 + F2. Operasi ini disebut jumlah vektor.

Bagaimana sahabat fisika asyik jika ingin menggambar jumlah dua buah vektor adalah dengan metode segitiga?

Pertama, gambar vektor F1 berupa tanda panah. kedua, gambar vektor kedua, F2, dengan pangkalnya berhimpitan dengan ujung vektor pertama, F1. ketiga, jumlahkan kedua vektor, dengan menggambar vektor resultan (F1 + F2), dari pangkal vektor F1 menuju ujung vektor F2. selesai. Proses ini ditunjukkan pada gambar di bawah ini.

Sahabat fisika asyik, cara menggambar selisih vektor pada dasarnya sama dengan menggambar penjumlahan dua vektor. 

Sebagai contoh, sebuah vektor F1 dan vektor F2 nilainya seperti tampak pada diagram di bawah. 

Berapa selisih kedua vektor tersebut? misalnya F3 adalah selisih vektor F1 dan F2, maka dapat kita tulis F3 = F1 – F2 atau F3 = F1 + (-F2). Hal ini menunjukkan bahwa selisih antara vektor F1 dan F2 sama saja dengan penjumlahan vektor F1 dan vektor -F2. tanda minus hanya menunjukkan bahwa arah -F2 berlawanan dengan F2. Bingung ? silahkan baca terus biar paham.

Bagaimana Sahabat Fisika Asyik menggambar selisih vektor F1 dan F2 ?

Pertama, gambar terlebih dahulu tanda panah yang melambangkan vektor F1. 

kedua, gambar vektor -F2. vektor -F2 besarnya sama dengan F2, hanya arahnya berlawanan. (Lihat dan bandingkan gambar di bawah dan di atas). 

Ketiga, gambar tanda panah vektor resultan F3, di mana pangkal vektor F3 berimpit dengan pangkal vektor F1 dan ujung vektor F3 berimpit dengan ujung vektor -F2. Berimpit itu artinya menempel, atau apalah terserah kamu . Selesai….

Gampang to sahabat fisika asyik? masih ga mudeng ? ulangi dari awal, bacanya pelan2 biar ngerti. Kalau sudah paham, lanjut, next mission…..katakan fisika harus asyik dulu :D

Menggambar Penjumlahan lebih dari 2 Vektor dengan metode Poligon

Poligon itu artinya segi banyak/banyak segi. Gimana, dah siap belum? sekarang tarik napas panjang….

Sebelumnya, sahabat fisika asyik belajar menggambar 2 vektor dengan cara segitiga. Bagaimana jika sahabat fisika asyik disuruh menggambar resultan atau jumlah vektor yang lebih dari 3?

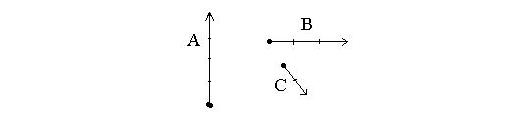
Misalnya kamu berpindah sejauh 4 meter, vektor A (lihat gambar di bawah), lalu kamu berpindah lagi sejauh 3 meter, vektor B. Karena hobimu jalan-jalan, maka kamu pindah lagi sejauh 2 meter, vektor C. karena suka jalan-jalan maka kamu dihukum pacarmu (aneh ya…) untuk menggambar vektor perpindahanmu tadi. Loncat ke bawah….

untuk menggambar vektor resultan/hasil penjumlahan lebih dari 2 vektor, maka kamu tidak bisa menggunakan metode/cara segitiga. Kenapa? 

Cari tahu sendiri ya, kan sahabat fisika asyik dah besar. Kamu harus menggunakan metode poligon/segi banyak. 

Caranya:

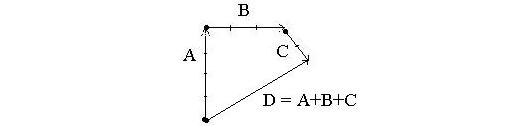
pertama, gambar vektor A. 

kedua, gambar vektor B, di mana pangkal vektor B berimpit/nempel dengan ujung vektor A (lihat gambar di bawah). 

Ketiga, gambar vektor C di ujung vektor B. caranya seperti menggambar vektor B. terakhir, gambar vektor D sebagai vektor resultan/hasil, dimana pangkal vektor D nempel dengan pangkal vektor A dan ujung vektor B nempel dengan ujung vektor C. selesai…

Kalo masih bingung, baca, sambil lihat gambar. Guampang to ? mission complete… lanjut.

Menggambar Penjumlahan 2 atau Lebih vektor dengan metode Jajaran Genjang.

Selain menggambar penjumlahan vektor dengan metode/cara segitiga dan poligon, kita juga bisa menggunakan metode jajaran genjong, eh genjang. Kalau metode segitiga khusus untuk dua vektor dan metode poligon khusus untuk lebih dari dua vektor, maka metode jajaran genjang untuk menggambar penjumlahan dua vektor atau lebih. 

Bagaimana menggambar penjumlahan dua vektor atau lebih menggunakan cara jajaran genjang ?

Menggambar penjumlahan 2 vektor menggunakan metode jajaran genjang

Misalkan dua orang anak mendorong sebuah benda dengan vektor Gaya masing-masing sebesar F1 dan F2, seperti ditunjukkan diagram di bawah. Ke arah mana benda itu akan pindah ?

untuk menggambar penjumlahan dua vektor, lakukan sesuai langkah2 di bawah ini. 

Pertama, gambar vektor F1 menggunakan tandah panah (lihat gambar di bawah). 

Kedua, gambar vektor F2, di mana pangkal/buntut berimpit/nempel dengan pangkal/buntut vektor F1.

ketiga, gambar vektor resultan, F3 (F1 + F2), di mana pangkal vektor F3 nempel dengan pangkal vektor F1 dan F2, sedangkan ujung vektor F3 nempel dengan titik temu garis putus-putus dari kedua ujung vektor F1 dan vektor F2 (sambil lihat gambar, biar tidak bingung).

Menggambar penjumlahan lebih dari 2 vektor menggunakan metode jajaran genjang.

Misalnya kamu berpindah sejauh 4 meter seperti vektor A (lihat gambar di bawah), lalu kamu berpindah lagi sejauh 3 meter seperti vektor B. 

Karena hobimu jalan-jalan, maka kamu pindah lagi sejauh 2 meter seperti vektor C. karena suka jalan-jalan maka kamu dihukum pacarmu (aneh ya…) untuk menggambar vektor perpindahanmu, tapi kali ini dengan metode jajaran genjong. Bagaimanakah ?

Untuk menggambar penjumlahan lebih dari 2 vektor, lihat petunjuk berikut ini. 

Pertama, gambar vektor A menggunakan tandah panah (lihat gambar di bawah). 

Kedua, gambar vektor B, di mana pangkalnya berimpit/nempel dengan pangkal/buntut vektor A.

ketiga, gambar vektor C, di mana pangkalnya berhimpit dengan pangkal vektor A dan B. 

keempat, buat garis putus-putus tegak lurus dari ujung vektor A dan B sampai kedua garis putus-putus tersebut bertemu, Vektor D (buat garis satu2, kalo kamu kidal+, pake aja dua tanganmu sekalian, hehe…). 

Kelima, tarik garis dari pangkal vektor A,B dan C menuju titik temu garis putus-putus yang sudah kamu buat tadi (jangan lupa lihat gambar ya). 

Keenam, buat lagi garis putus2 tegak lurus dari titik temu vektor A dan B dan dari ujung vektor C sampai kedua garis putus2 tersebut bertemu. Nah, sekarang tarik garis lurus dari pangkal vektor A, B dan C menuju titik temu garis putus2 yang baru saja kamu buat, Vektor Resultan (R). 

Garis terakhir tersebut adalah vektor resultannya….

Tadi kita belajar menggambar resultan penjumlahan vektor, sekarang kita belajar menentukan besar dan arah vektor resultan.